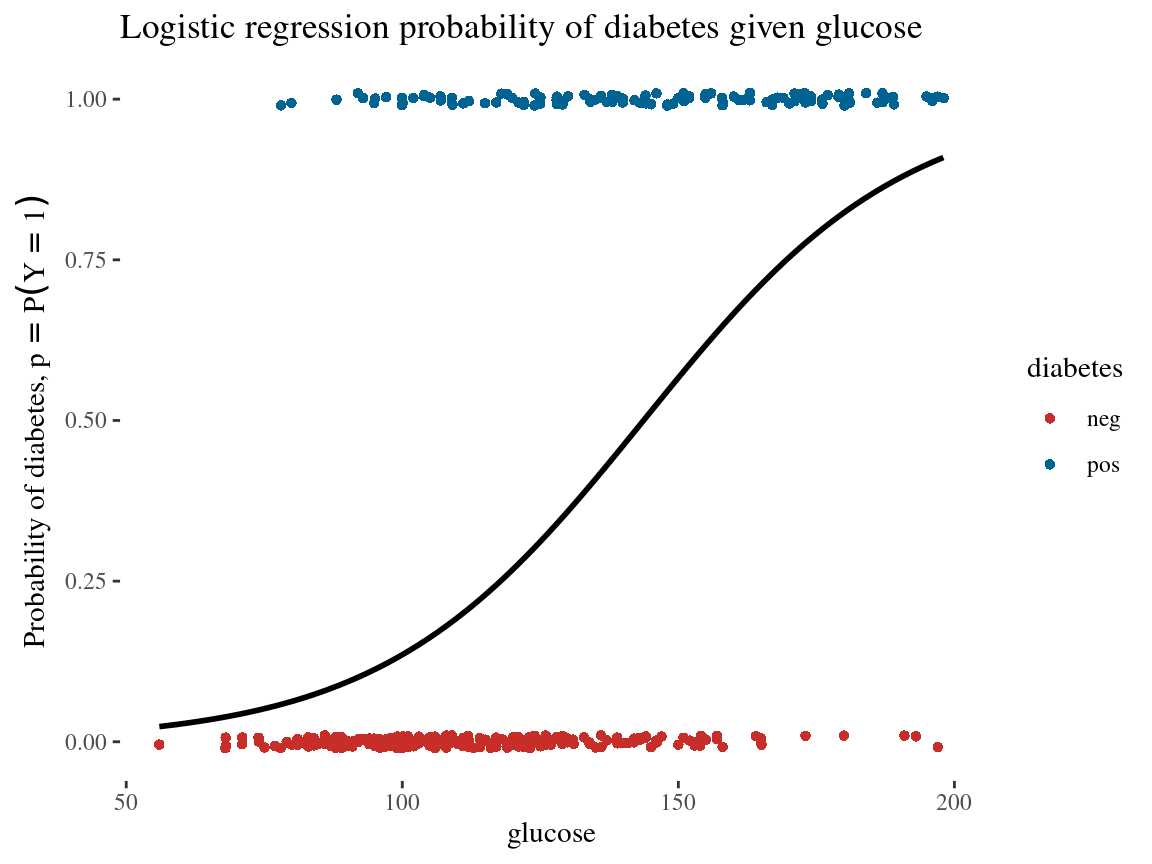
Logistic Regression
STAT 220
Bastola
Classification using simple logistic regression
- Goal: Understand why logistic regression is used for categorical outcomes.
- Context: Traditional linear regression is limited to continuous outcomes.
- Solution: Logistic regression models the probability of a categorical outcome.
Why Not Linear Regression?
- Issue with categorical outcomes: Predictions can fall outside the \([0,1]\) range.
- Consequence: Nonsensical probability predictions for binary outcomes \((Y=0\text{ or }Y=1)\)).
Introduction to Logistic Regression
- Solution: Transform the outcome into a format that linear regression can handle.
- Method: Model the log odds of the probability of success versus failure.
From Probability to Odds
- Probability: Chance of success (\(Y=1\)) over total possibilities. \[P(Y=1)=\frac{\text { number of successes }}{\text { total trials }}\]
- Odds: Ratio of the probability of success to the probability of failure. \[Odds =\frac{P(Y=1)}{1-P(Y=1)}\]
Logit Transformation
- Goal: Convert odds to a continuous scale that can span negative to positive infinity.
- Logit Function: Natural logarithm of the odds. \[\log \left(\frac{P(Y=1)}{1-P(Y=1)}\right)\]
- Why? Makes it possible to use linear regression techniques.
- Binary response, \(Y\), with an explanatory (predictor, features) variables, \(X_1\).
- We model the probability that \(Y\) belongs to a particular category.
\[P(Y = 1 ) = \frac{e^{\beta_0 + \beta_1X_1}}{1 + e^{\beta_0 + \beta_1X_1}}\]
\[\text{Odds} = \frac{P(Y = 1 )}{1 - P(Y = 1 )} = e^{\beta_0 + \beta_1X_1}\]
\[\text{Log Odds} = \beta_0 + \beta_1X_1\]
# Create data split for train and test
set.seed(12345) # Ensures reproducibility of the data split
db_single <- db %>%
select(diabetes, glucose) %>%
# Relevels 'diabetes' factor to ensure 'neg' comes before 'pos'
mutate(diabetes = fct_relevel(diabetes, c("neg", "pos")))
db_split <- initial_split(db_single, prop = 0.80)
db_train <- db_split %>% training()
db_test <- db_split %>% testing() Tidy the Summary
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -5.61 0.678 -8.28 1.20e-16
2 glucose 0.0392 0.00514 7.62 2.55e-14\[\log \left(\frac{p}{1-p}\right)=-5.61+0.0392 \cdot \text { glucose }\]
Where \(p = P(Y = 1)\) is the probability of having diabetes
Interpreting Coefficients: Log Odds
- Coefficient Meaning: Change in log odds of the outcome for a one-unit increase in the predictor.
A coefficient of 0.0392 for glucose means…
…a one-unit increase in glucose level increases the log odds of diabetes by 0.0392.
Exponentiating Coefficients: Odds Ratios
\[Odds = \frac{probability}{1 - probability}\]
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.00364 0.678 -8.28 1.20e-16
2 glucose 1.04 0.00514 7.62 2.55e-14\[\text { Odds }=0.00364 \times(1.04)^{\text {glucose }}\]
An odds ratio of 1.04 means that for each additional unit of glucose, the odds of having diabetes increase by 4%.
Understanding Odds Ratios: Summary
- Transformation: Turning log-odds coefficients into odds ratios.
- Odds Ratio \(=e^{\beta_i}\)
- Interpretation: For each unit increase in the predictor, the odds multiply by the odds ratio.
Importance of Scaling and Centering
db_recipe <- recipe(diabetes ~ ., data = db_train) %>%
step_scale(all_numeric_predictors()) %>%
step_center(all_numeric_predictors()) %>%
prep()- Ensures all features contribute equally to model calculations.
- Helps gradient descent algorithms converge more quickly.
- Standardizes coefficient scales, improving model interpretability.
Group Activity 1

- Please clone the
ca24-yourusernamerepository from Github - Please do problem 1 in the class activity for today
10:00 Threshold for classification
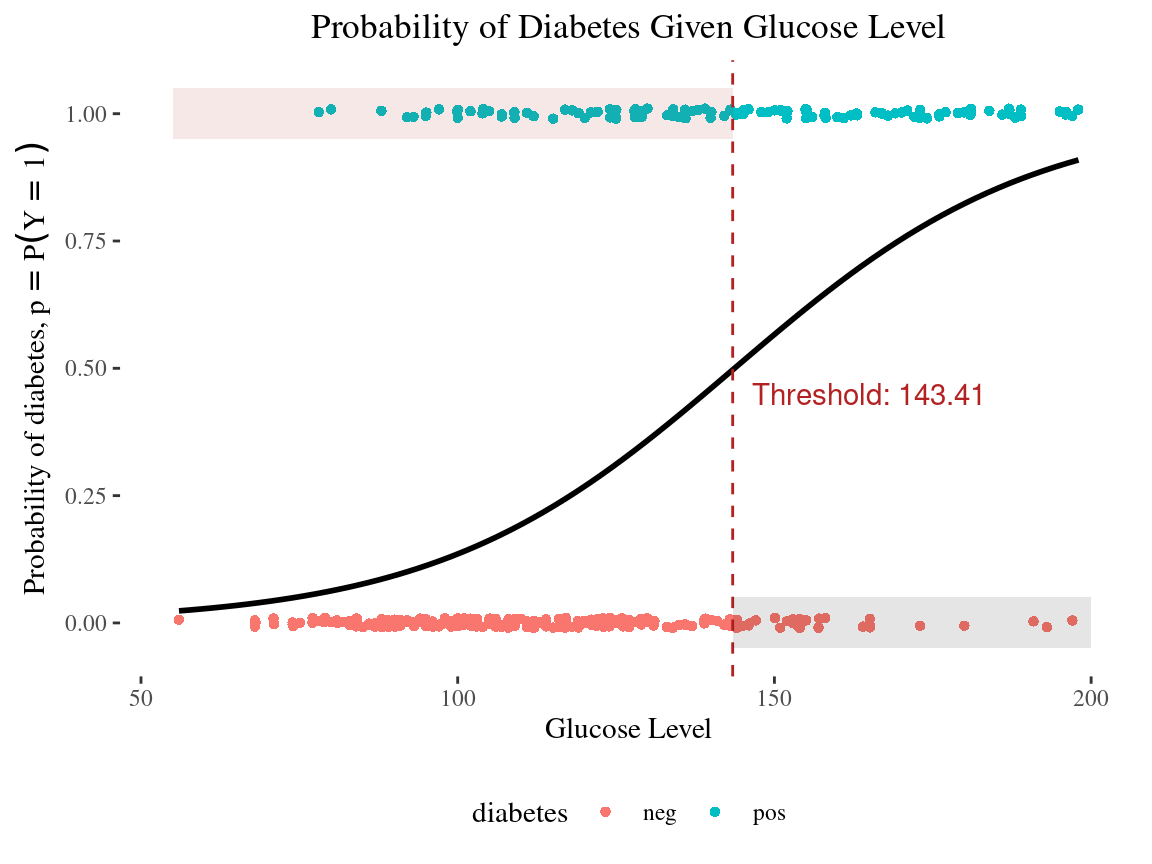
Class Prediction
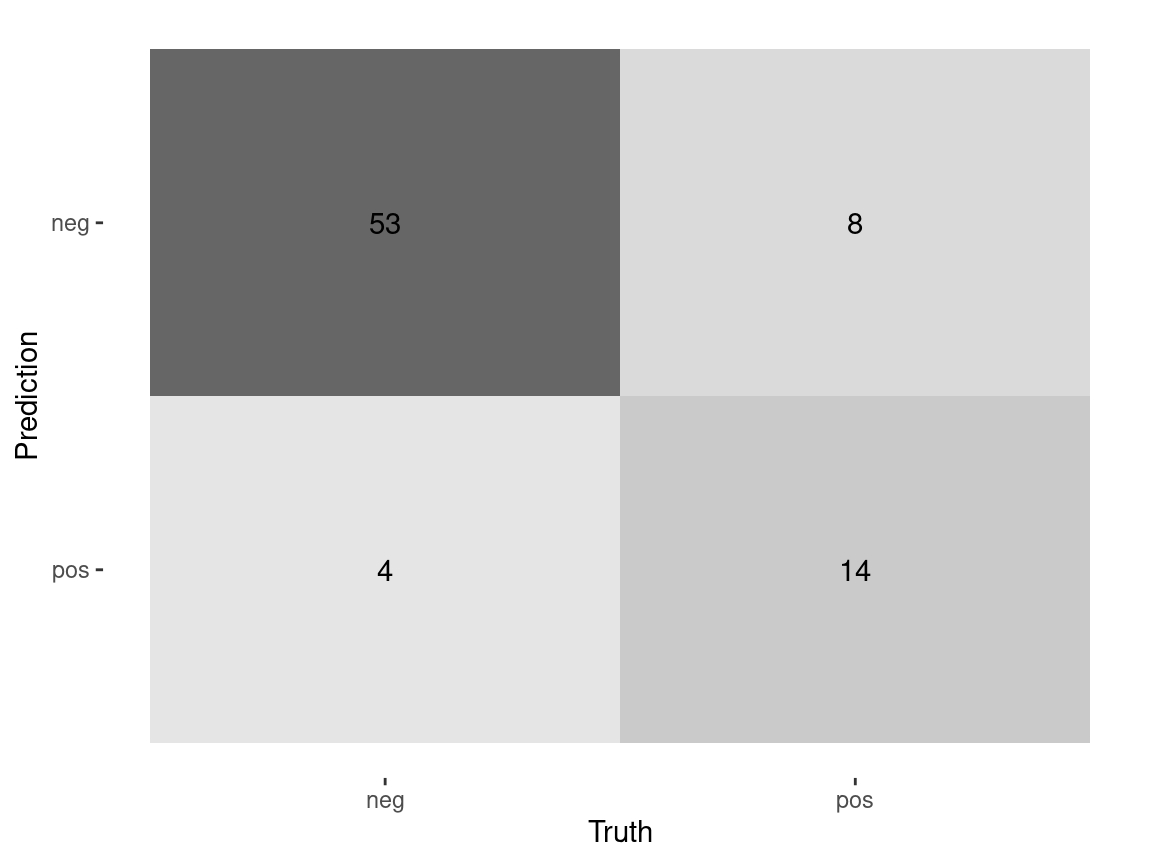
Class Probabilities with threshold = 0.30
# Prediction Probabilities
library(probably)
pred_prob <- predict(fitted_logistic_model,
new_data = db_test,
type = "prob")
db_results <- db_test %>% bind_cols(pred_prob) %>%
mutate(.pred_class = make_two_class_pred(.pred_neg,
levels(diabetes),
threshold = .30)) %>%
select(diabetes, glucose, contains(".pred")) diabetes glucose .pred_neg .pred_pos .pred_class
25 pos 143 0.5040090 0.49599103 neg
52 neg 101 0.8402912 0.15970881 neg
60 neg 105 0.8181391 0.18186086 neg
64 neg 141 0.5235673 0.47643271 neg
69 neg 95 0.8693592 0.13064080 neg
83 neg 83 0.9141287 0.08587128 neg
98 neg 71 0.9445349 0.05546507 neg
110 pos 95 0.8693592 0.13064080 neg
135 neg 96 0.8648480 0.13515203 neg
143 neg 108 0.8000067 0.19999330 negCustom Metrics
custom_metrics <- metric_set(accuracy,
sensitivity,
specificity,
ppv)
custom_metrics(db_results,
truth = diabetes,
estimate = .pred_class)# A tibble: 4 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 0.823
2 sensitivity binary 0.982
3 specificity binary 0.409
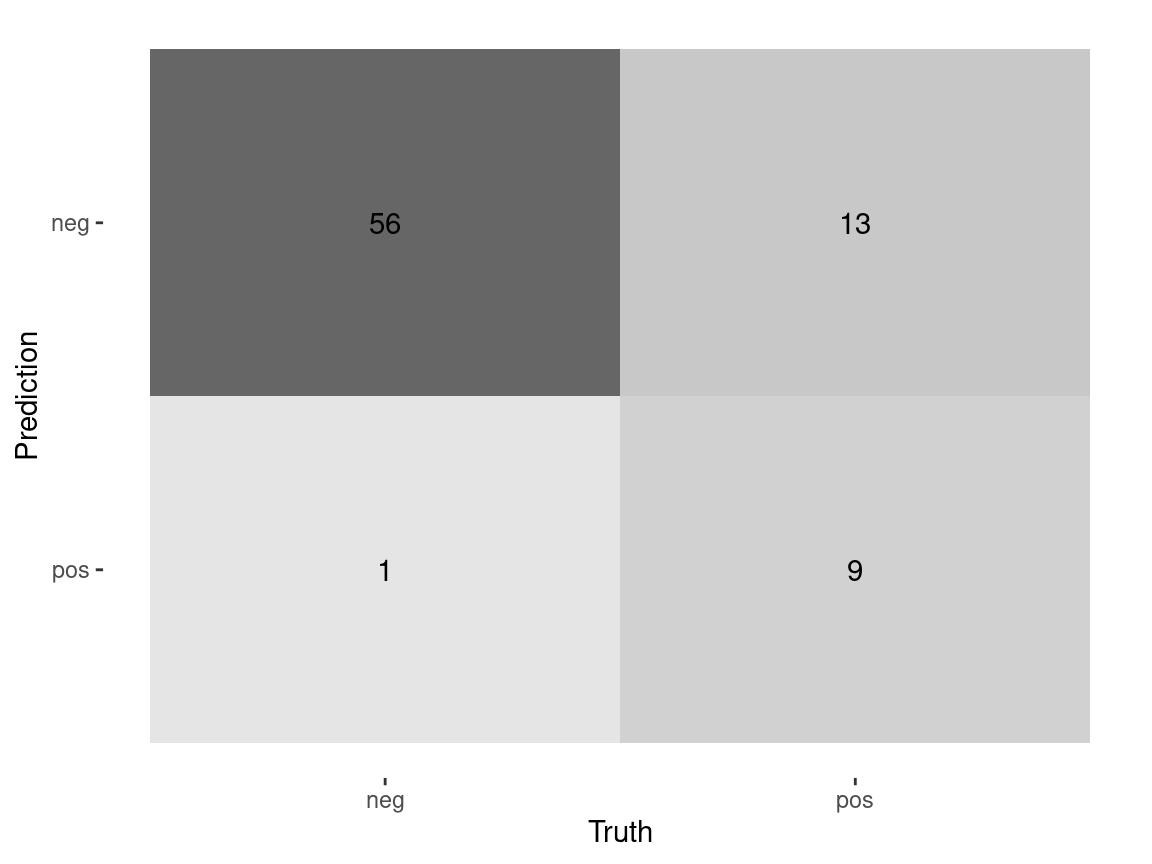
4 ppv binary 0.812Class Probabilities with threshold = 0.70
# Prediction Probabilities
library(probably)
pred_prob <- predict(fitted_logistic_model,
new_data = db_test,
type = "prob")
db_results <- db_test %>% bind_cols(pred_prob) %>%
mutate(.pred_class = make_two_class_pred(.pred_neg,
levels(diabetes),
threshold = .70)) %>%
select(diabetes, glucose, contains(".pred")) diabetes glucose .pred_neg .pred_pos .pred_class
25 pos 143 0.5040090 0.49599103 pos
52 neg 101 0.8402912 0.15970881 neg
60 neg 105 0.8181391 0.18186086 neg
64 neg 141 0.5235673 0.47643271 pos
69 neg 95 0.8693592 0.13064080 neg
83 neg 83 0.9141287 0.08587128 neg
98 neg 71 0.9445349 0.05546507 neg
110 pos 95 0.8693592 0.13064080 neg
135 neg 96 0.8648480 0.13515203 neg
143 neg 108 0.8000067 0.19999330 negCustom Metrics

custom_metrics <- metric_set(accuracy,
sensitivity,
specificity,
ppv)
custom_metrics(db_results,
truth = diabetes,
estimate = .pred_class)# A tibble: 4 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 0.785
2 sensitivity binary 0.754
3 specificity binary 0.864
4 ppv binary 0.935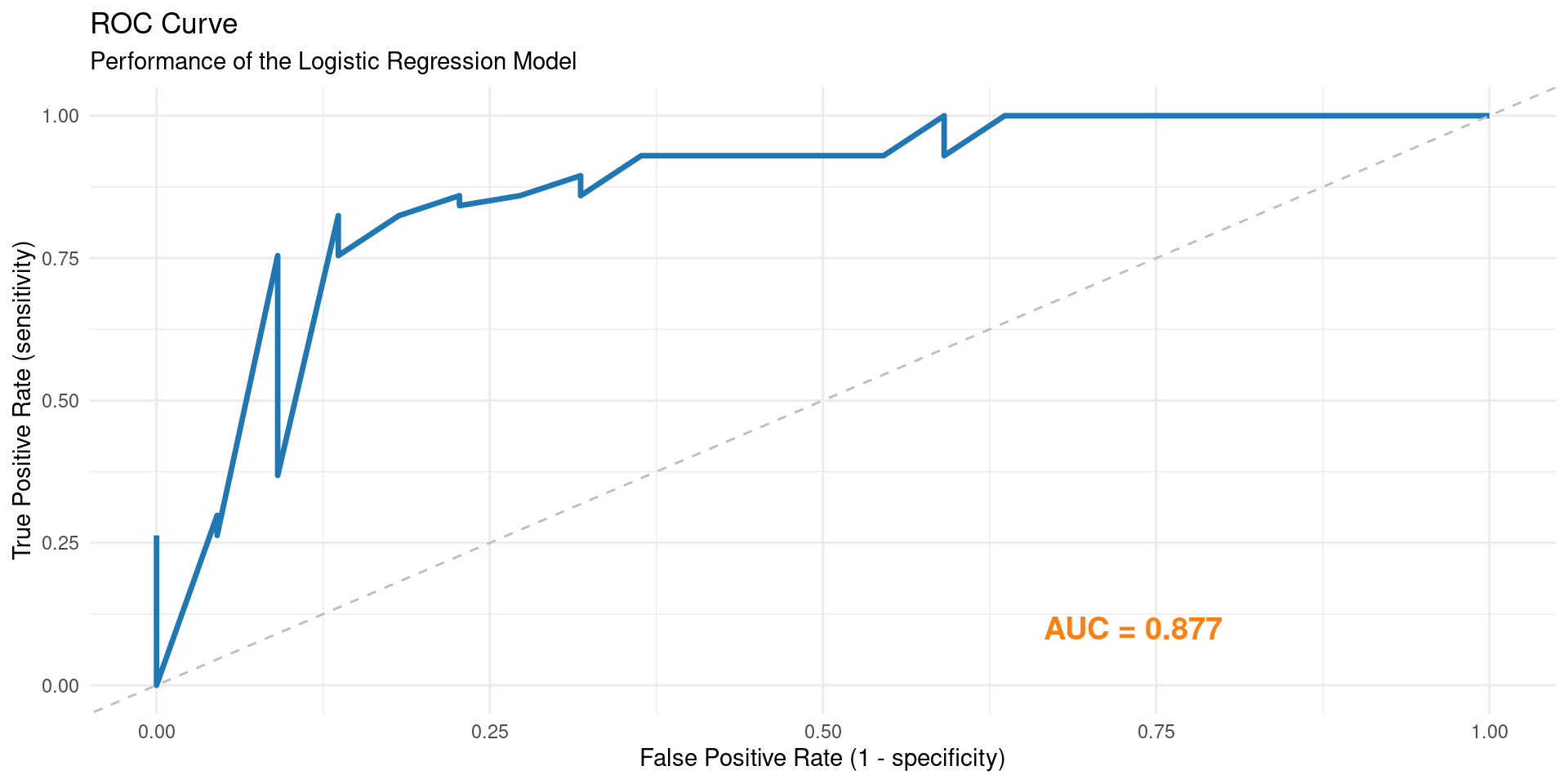
library(yardstick)
diabetes_prob <- predict(fitted_logistic_model, db_test, type = "prob")
diabetes_results <- db_test %>% select(diabetes) %>% bind_cols(diabetes_prob)
diabetes_results %>%
roc_curve(truth = diabetes, .pred_neg) %>%
ggplot(aes(x = 1 - specificity, y = sensitivity)) +
geom_line(color = "#1f77b4", size = 1.2) +
geom_abline(linetype = "dashed", color = "gray") +
annotate("text", x = 0.8, y = 0.1, label = paste("AUC =", round(roc_auc(diabetes_results, truth = diabetes, .pred_neg)$.estimate, 3)), hjust = 1, color = "#ff7f0e", size = 5, fontface = "bold") +
labs(title = "ROC Curve", subtitle = "Performance of the Logistic Regression Model", x = "False Positive Rate (1 - specificity)", y = "True Positive Rate (sensitivity)") +
theme_minimal()Exact Optimal Threshold
# A tibble: 58 × 3
.threshold specificity sensitivity
<dbl> <dbl> <dbl>
1 -Inf 0 1
2 0.106 0 1
3 0.113 0.0455 1
4 0.154 0.0909 1
5 0.159 0.182 1
6 0.187 0.227 1
7 0.193 0.273 1
8 0.199 0.318 1
9 0.218 0.364 1
10 0.239 0.409 1
# ℹ 48 more rowsExact Optimal Threshold
# Compute the ROC curve
roc_curve(diabetes_results, truth = diabetes, .pred_neg) %>%
# Look for the point where specificity is 0.87 and sensitivity is 0.76
arrange(abs(specificity - (1 - 0.13)), abs(sensitivity - 0.76)) # A tibble: 58 × 3
.threshold specificity sensitivity
<dbl> <dbl> <dbl>
1 0.706 0.864 0.754
2 0.698 0.864 0.772
3 0.690 0.864 0.807
4 0.681 0.864 0.825
5 0.714 0.909 0.754
6 0.738 0.909 0.737
7 0.745 0.909 0.719
8 0.760 0.909 0.702
9 0.767 0.909 0.684
10 0.774 0.909 0.667
# ℹ 48 more rowsExact Optimal Threshold
# Compute the ROC curve
roc_curve(diabetes_results, truth = diabetes, .pred_neg) %>%
# Find point where specificity is 0.87 and sensitivity is 0.76
arrange(abs(specificity - (1 - 0.13)), abs(sensitivity - 0.76)) %>%
slice(1)# A tibble: 1 × 3
.threshold specificity sensitivity
<dbl> <dbl> <dbl>
1 0.706 0.864 0.754Group Activity 2

- Please finish the remaining problems in the class activity for today
10:00